Origin of the word Holor¶
The name of the library pays homage to the work of Parry Moon and Domina Eberle Spencer, who coined the term Holor:
The word holor indicates a mathematical entity that is made up of one or more independent quantities. Examples of holors are complex numbers, vectors, matrices, tensors, and other hypernumbers.
-- Parry Moon and Domina Eberle Spencer 1
Moon and Spencer define holors (from the Greek ὅλος, a whole) as collections of indipendent elements, or merates (from the Greek μέρος, a part). In their definition, holors are characterized by two fundamental qualities:
- valence \(N\): which indicates the number of dimensions.
- plethos \(n_i\): which indicates the number of elements in the \(i\)-th dimension.
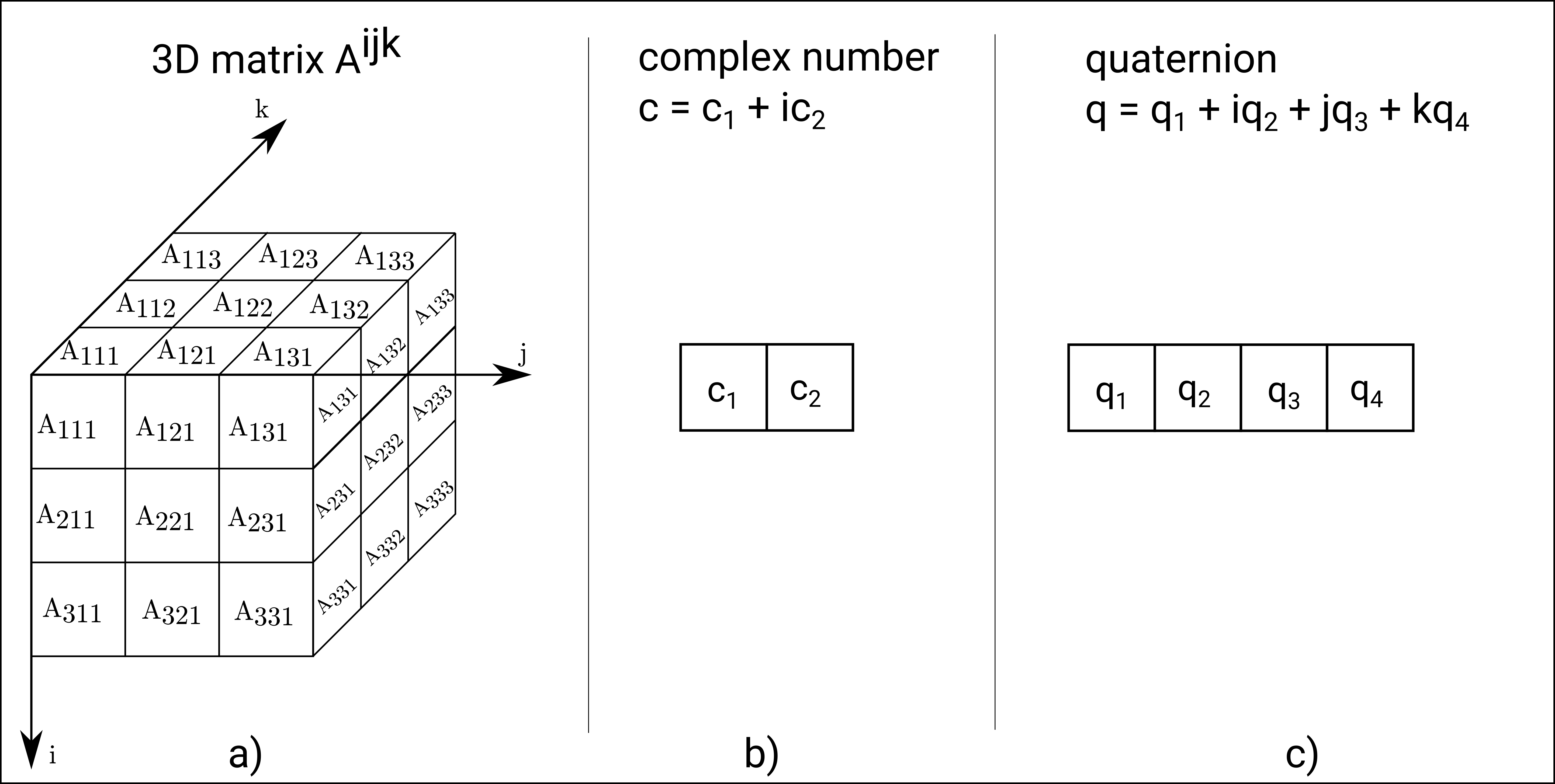
Moon and Spencer also introduce a general index notation to identify the merates of a holor: a single dimensional holor with three merates is denoted as \(v^i = (v^1, v^2, v^3)\), a bi-dimensional holor with \(2 \times 2\) elements is denoted as \(A^{ij} = (A^{1,1}, A^{1,2}, A^{2,1}, A^{2,2})\), and so on. The definition of holors is purposedly broad so as to encompass under a unique formulation a large number of mathematical entities, such as matrices, tensors, complex numbers, quaternions, etcetera. Figure 1 illustrates some examples of holors.
The Theory of Holors goes further to elaborate an algebra of holors, an operation called \(\gamma\)-product that allows to modify the characteristics (valence, positions of indices, symmetry or antisymmetry) of holors, transformations. It also provides definitions for notable classes of holors, like tensors, akinetors, oudors.